Металлические конструкции

Основы расчета металлических конструкций

Эта статья является частью проектного курса, который обучает слушателя правильному выбору расчетных схем, сбору нагрузок, моделированию и расчету строительных конструкций. Применение САПР в рамках курса сознательно сведено к минимуму, чтобы слушатель научился проектировать элементы конструкции «вручную». Чем сложнее проектируемое здание или сооружение, тем сложнее проектировщику фокусироваться на одном-единственном строительном материале. Даже если в конструкции преобладает железобетон, то Вам вряд ли удастся полностью избежать работы со стальными элементами, и наоборот (если, конечно, Вы не отдадите эту работу другим специалистам или на аутсорс).

Рисунок 1. Металлическая конструкция

В чем основные достоинства металлоконструкций? Как правило, они существенно легче и одновременно прочнее изделий из бетона. Стальные конструкции технологичны: их достаточно просто изготовить, транспортировать, монтировать. Наконец, конструкциям из стали можно придать более изящные и ажурные формы, по сравнению с массивными железобетонными конструкциями.

Но, помимо достоинств, есть и недостатки. Стальные конструкции достаточно «капризны» — за ними нужен соответствующий уход (беречь от коррозии, следить за температурным режимом, устранять мелкие дефекты и пр.).

Что легче считать?

Начинающие проектировщики нередко задают вопрос: что легче рассчитывать, железобетон или металл?

Уверен, Вы уже догадались: однозначно ответить на этот, казалось бы, простой вопрос — нельзя. Давайте разберемся, почему.

Сталь обладает однородностью свойств. С точки зрения расчета и общего понимания, как будет деформироваться, например, стальной стержень, это несомненный плюс. То, что сталь одинаково работает во всех направлениях (изотропный материал), делает элементы металлоконструкций как бы более «прогнозируемыми», понятными. Действительно, какая нам разница, в какую сторону деформировалась стальная балка?

Рисунок 2. Упругая работа стальной балки: при одинаковом усилии имеем одинаковое изменение длины Но давайте взглянем на объем документов [1] и [4]. Нельзя не заметить, что стандарты проектирования стальных конструкций существенно объемнее норм проектирования ЖБК. С чего бы это, если мы имеем дело с вполне предсказуемым строительным материалом?

Дело в том, что разнообразие форм и видов металлоконструкций порождает множество различных схем работы, стадий НДС, вариантов соединений конструктивных элементов и прочих аспектов. Да, такие системы, в общем случае, рассчитываются формулами сопротивления материалов, но почти все эти формулы уточнены различными коэффициентами. Коэффициентов — много (как говорится, «на все случаи жизни»), и основаны они на множестве натурных и численных экспериментов.

Главная роль коэффициентов в «сниповских» формулах — согласовать методику допустимых напряжений с методикой предельных состояний. В определении этих коэффициентов зачастую и заключается основная сложность расчетов, и Вам следует хорошенько к этому подготовиться.

Схемы металлических конструкций

Большинство металлоконструкций реализовано по балочно-стержневой схеме. Как правило, это системы перекрестных балок, прогонов, колонн, связей и других элементов. Решетки стальной конструкции и крепления элементов могут быть простыми или сложными, но в подавляющем большинстве зданий из металла прослеживается общая стержневая структура:

Рисунок 3. Различные схемы металлоконструкций

Существуют отдельные классы висячих и мембранных покрытий, канатных конструкций и прочих «экзотических» систем, однако жестко соединенные стержневые элементы (каркас) — основа большинства зданий и сооружений из стали. А раз это так, то и расчет подобных систем вполне оправданно выполнять по теории стержневых систем.

Напомню, что «балкой» в строительной механике принято называть элемент, работающий преимущественно на изгиб, а «стержнем» — на растяжение-сжатие.

Расчет металлоконструкций очень тесно связан с определением напряжений. Напряжение — это усилие взаимодействия между микрочастицами материала, которое помогает элементу сопротивляться внешним нагрузкам и не развалиться на части.

В разных точках конструкции могут возникать разные напряжения. Это обусловлено тремя измерениями, в которых мы живем, свойствами материала и геометрией элемента, а также схемой нагружения.

На практике чаще всего мы будем иметь дело с нормальными и ненормальными касательными напряжениями.

Нормальное напряжение

Нам понадобится декартова система координат. Пусть ось xx этой системы совпадает с нейтральной осью балки, а оси yy и zz будут главными осями сечения.

Рисунок 4. Двутавровая балка, ее система координат; вертикальная и продольная нагрузки

Под действием вертикальной нагрузки в нормальном сечении балки появится нормальное напряжение:

σ=MW,(1)σ=MW,(1)

где

• MM — изгибающий момент, действующий в данном сечении;
• WW — момент сопротивления.

Под действием продольной нагрузки (сжимающей или растягивающей) в нормальном сечении балки появится соответствующее нормальное напряжение:

σ=FA,(2)σ=FA,(2)

где

• FF — усилие в элементе;
• AA — площадь поперечного сечения.

Присмотритесь к формулам (1) и (2). Они очень похожи: в числителе располагается внутреннее усилие (момент или сила), зависящее только от внешней нагрузки, а в знаменателе — соответствующая геометрическая характеристика, зависящая только от геометрии сечения. Таким образом, напряжение как бы характеризует степень «нагруженности» сечения.

Как определить момент сопротивления балки

Момент сопротивления — геометрический параметр сечения, характеризующий сопротивляемость в процессе изгиба:

W=Jyz,(3)W=Jyz,(3)

где

• JyJy — центральный момент инерции относительно оси изгиба (в данном случае — оси y);
• zz — расстояние от центра тяжести сечения до точки, в которой определяется момент сопротивления (по высоте).

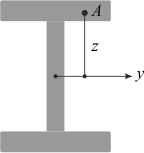Рисунок 5. К расчету момента сопротивления и нормального напряжения Таким образом, чтобы определить наиболее опасные (максимальные) напряжения в изгибаемой стальной балке, необходимо построить эпюру нормальных напряжений по всей высоте сечения: 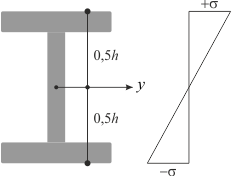      Рисунок 6. Эпюра нормальных напряжений

Как выбрать знак напряжения?

Наибольшие по модулю, но противоположные по знаку напряжения для двутаврового сечения будут в его крайних точках (рис. 6) — как раз там, где плечо zz — максимальное (3). С физической точки зрения это — наиболее нагруженные волокна, которые получат наибольшие деформации. Смысл выражения «разные по знаку напряжения» должен быть очевиден: напряжение одного знака характеризует сжатие, другого — растяжение.

Как нет единственно верного правила знаков для сил и моментов, так нет его и для напряжений. В каждом конкретном случае Вы можете установить свое правило или следовать правилам, заложенным в конкретную САПР.

Что делать, если балка изгибается в другой плоскости?

Если балка изгибается, например, в горизонтальной плоскости, то принцип расчета напряжений остается прежним. Единственное, на что следует обратить внимание, — это геометрия: какая из осей теперь будет осью изгиба.

Рисунок 7. Горизонтальная нагрузка и соответствующая эпюра изгибающих моментов

На рисунке 7 ось изгиба — это ось zz. Соответственно, геометрические характеристики теперь следует определять относительно этой оси.

Рисунок 8. Эпюра напряжений при изгибе в горизонтальной плоскости

По сравнению с расчетом в вертикальной плоскости эта ситуация встречается в практике проектирования существенно реже.

σ=MzW=MzJzy.(4)σ=MzW=MzJzy.(4)

Касательное напряжение

Касательное напряжение направлено вдоль той же оси, что и поперечная сила, и связано с ней следующим соотношением (формула Журавского):

τ=Q⋅Sb⋅J,(5)τ=Q⋅Sb⋅J,(5)

где

• QQ — поперечная сила, действующая в сечении;
• SS — статический момент той части сечения, которая расположена выше рассматриваемой точки (отсечена);
• bb — ширина сечения на уровне исследуемой точки;
• JJ — изгибный момент инерции сечения.

Основываясь на формуле (5), получим соотношения для изгиба в вертикальной плоскости (первая формула) и в горизонтальной плоскости (вторая формула):

τz=Qz⋅Sb⋅Jy;τy=Qy⋅Sb⋅Jz.(6)τz=Qz⋅Sb⋅Jy;τy=Qy⋅Sb⋅Jz.(6)

Рисунок 9. Нагружение балки в разных плоскостях

Эпюра касательных напряжений

Рассмотрим, как построить эпюру касательных напряжений на примере того же двутаврового сечения. Рисунок 10. К построению эпюры касательных напряжений Чтобы вычислить касательное напряжение в точке AA (рис. 10, 1), сначала определим статический момент отсеченной части сечения (она показана на рисунке зеленым цветом). Статический момент равен произведению площади отсеченной части на расстояние от ее центра тяжести до центра тяжести всего сечения:

S=(b⋅h+t⋅H)z.(7)S=(b⋅h+t⋅H)z.(7)

Касательное напряжение в точке AA:

τA=Q⋅St⋅J.(8)τA=Q⋅St⋅J.(8)

Аналогично, статический момент для определения касательного напряжения в точке BB:

S=b⋅h⋅z.(9)S=b⋅h⋅z.(9)

Касательное напряжение в точке BB (рис. 10, 2):

τB=Q⋅Sb⋅J.(10)τB=Q⋅Sb⋅J.(10)

Обратите внимание, что поперечная сила QQ и момент инерции сечения JJ в рамках одного сечения — неизменны.

Расчет металлоконструкций по нормам проектирования СНиП, Еврокод

Как уже было сказано, все основные расчеты в нормах проектирования стальных конструкций основаны на формулах сопротивления материалов, но с адаптацией под методику предельных состояний.

Кейс. Расчет оттяжки мачтовой конструкции

Цель данного кейса — спроектировать оттяжку под вертикальный столб высотой H=28H=28 м. Сечение мачты — два двутавра Д40, соединенных под прямым углом (рисунок 11).

Рисунок 11. Кейс по расчету мачтовой оттяжки: 1 — фасад; 2 — план

Как правило, оттяжки мачтовых конструкций в плане располагаются по кругу, через 120° (рис. 11, 2) или чаще. В любом случае достаточно сконструировать одну такую оттяжку, а остальные принять идентичными.

Примем, что оттяжка будет состоять из 7 высокопрочных проволок в соответствии со стандартом [9]. Диаметр центральной проволоки равен 4,0 мм, шести остальных — 3,8 мм. Полезная площадь сечения всего каната составляет (см²):

A=π4(0,402+6⋅0,382)=0,81.(11)A=π4(0,402+6⋅0,382)=0,81.(11)

Примем также, что оттяжка будет крепиться к мачте на высоте h=20h=20 м от земли и на a=16a=16 м отстоять от нее в плане. Тросовый элемент работает только на растяжение (изгибные и сжимающие усилия в нем не возникают), поэтому оттяжка будет растягиваться, только когда мачта отклоняется в сторону — например, от поперечной ветровой нагрузки. Рисунок 12. К расчету мачты с оттяжкой: 1 — расчетная схема; 2 — ветровая нагрузка и линия влияния усилия в оттяжке

В данном примере ограничимся лишь основным типом ветровой нагрузки, без резонансных и других аэродинамических эффектов. Не будем также включать в расчетную схему собственный вес мачты, так как оттяжка, скорее всего, была подтянута в анкерном устройстве до расчетного усилия и включилась в работу уже после того, как мачта «просела» под собственным весом.

Данная система — статически неопределима, поэтому для ее расчета логично применить МКЭ. Построим линию влияния усилия RR от единичной силы, которая движется снизу вверх по мачте со стороны, обдуваемой ветром. График изменения такого усилия показан на рис. 12, 2. Если бы можно было принять ветровую нагрузку равномерно распределенной по высоте мачты, то достаточно было бы умножить интенсивность этой нагрузки на суммарную площадь линии влияния (в данном примере площадь линии влияния составляет 27,04 м). Но ветровая нагрузка меняет свое значение в зависимости от того, на какой высоте мы ее прикладываем [7]:

w=wm+wp=w0k(ze)c(1+ζ(ze)ν).(12)w=wm+wp=w0k(ze)c(1+ζ(ze)ν).(12)

Обратите внимание, что как минимум два параметра в (12) зависят от высоты приложения нагрузки [7]. Чтобы выполнить расчет как можно точнее, необходимо разделить мачту на небольшие отрезки по высоте и для каждого отдельного отрезка определить соответствующую равнодействующую ветровой нагрузки.

Не забываем также, что в СНиП «Нагрузки и воздействия» [7] давление ветра указано в килопаскалях (кПа). Чтобы превратить плоскостное давление в погонную нагрузку (кН/м), умножаем его на ширину поверхности, обдуваемой ветром:

Не забываем также, что в СНиП “Нагрузки и воздействия” [7] давление ветра указано в кПа. Чтобы превратить плоскостное давление в погонную нагрузку (кН/м), умножаем его на ширину поверхности, обдуваемой ветром: Рисунок 13. К сбору ветровой нагрузки

q=w⋅b.(13)q=w⋅b.(13)

Результирующее усилие в оттяжке будет равно:

R=∑qi⋅ωi,(14)R=∑qi⋅ωi,(14)

где

• qiqi — погонная ветровая нагрузка на i-м участке мачты, кН/м;
• ωiωi — площадь i-го участка линии влияния, м.

В СНиП «Стальные конструкции» [4] нет отдельных положений по расчету канатных элементов, но такие положения есть в 11-й части Еврокода 3. Так, условие прочности каната в EN 1993-1-11 выглядит следующим образом [8]:

FEdFRd≤1,(15)FEdFRd≤1,(15)

где

• FEdFEd — расчетное усилие в канате, кН (в данном кейсе это усилие RR);
• FRdFRd — расчетное сопротивление каната растяжению, кН.

В терминологии, традиционной для стран СНГ, расчетным сопротивлением обычно называют допустимое напряжение (единица измерения — МПа), но в формуле (15) под расчетным сопротивлением следует понимать усилие, максимально допустимое для каната:

FRd=Fuk1,5γR,(16)FRd=Fuk1,5γR,(16)

где

• FukFuk — нормативное значение разрывного усилия каната;
• γRγR — частичный коэффициент, равный 1,0 в случае, если анкерное крепление каната исключает появление опорных моментов, и 0,9 — если опорные моменты допустимы.

Значения частичного коэффициента (partial factor) 0,9 и 1,0 для расчета канатов по Еврокоду — рекомендованные, поэтому в конкретной стране они могут быть заменены на соответствующие значения из национального приложения. Отмечу, что в нормах [4] коэффициент надежности по материалу для канатов равен 1,6, что почти аналогично европейским нормам. Чтобы получить нормативное значение разрывного усилия каната, необходимо обратиться к сортаменту или спецификации завода-изготовителя. Как правило, там указываются два параметра:

• суммарное разрывное усилие всех проволок в канате;
• разрывное усилие каната в целом.

Важная особенность: разрывное усилие всего каната меньше, чем суммарное разрывное усилие всех проволок, из которых он состоит. Поэтому в расчет необходимо закладывать именно второе, меньшее значение. Нормативное значение разрывного усилия каната, применяемого в данном кейсе, составляет 101,0 кН [9]. Определяем расчетное значение, кН:

FRd=Fuk1,5γR=101,01,5⋅1,0=67,3.FRd=Fuk1,5γR=101,01,5⋅1,0=67,3.

Финальная проверка прочности оттяжки:

FEdFRd=RFRd=4,867,3=0,07<1.FEdFRd=RFRd=4,867,3=0,07<1.

Выводы

Для расчета большинства металлических конструкций могут быть применены стержневые и балочные расчетные схемы. В расчетах металлоконструкций Вы можете ориентироваться на отечественные или зарубежные нормы проектирования, а также сортаменты различных производителей стального проката. Но вне зависимости от того, какие нормы и стандарты Вы планируете применять, для корректного проектирования зданий и сооружений из стали Вам нужно обладать навыками сбора нагрузок, расчета усилий, а также определения нормальных и касательных напряжений.